topic_coherence.indirect_confirmation_measure – Indirect confirmation measure module

This module contains functions to compute confirmation on a pair of words or word subsets.

Notes

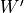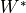The advantage of indirect confirmation measure is that it computes similarity of words in W' and W^{*} with respect to direct confirmations to all words. Eg. Suppose x and z are both competing brands of cars, which semantically support each other. However, both brands are seldom mentioned together in documents in the reference corpus. But their confirmations to other words like “road” or “speed” do strongly correlate. This would be reflected by an indirect confirmation measure. Thus, indirect confirmation measures may capture semantic support that direct measures would miss.

The formula used to compute indirect confirmation measure is

\widetilde{m}_{sim(m, \gamma)}(W', W^{*}) = s_{sim}(\vec{v}^{\,}_{m,\gamma}(W'), \vec{v}^{\,}_{m,\gamma}(W^{*}))

where s_{sim} can be cosine, dice or jaccard similarity and

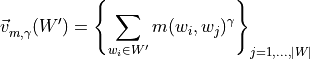
\vec{v}^{\,}_{m,\gamma}(W') = \Bigg \{{\sum_{w_{i} \in W'}^{ } m(w_{i}, w_{j})^{\gamma}}\Bigg \}_{j = 1,...,|W|}

class gensim.topic_coherence.indirect_confirmation_measure.ContextVectorComputer(measure, topics, accumulator, gamma)

Bases: object

Lazily compute context vectors for topic segments.

Parameters

  • measure (str) – Confirmation measure.

  • topics (list of numpy.array) – Topics.

  • accumulator (WordVectorsAccumulator or) – InvertedIndexAccumulator Word occurrence accumulator from probability_estimation.

  • gamma (float) – Value for computing vectors.

sim_cache

Cache similarities between tokens (pairs of word ids), e.g. (1, 2).

Type

dict

context_vector_cache

Mapping from (segment, topic_words) –> context_vector.

Type

dict

Example

>>> from gensim.corpora.dictionary import Dictionary
>>> from gensim.topic_coherence import indirect_confirmation_measure, text_analysis
>>> import numpy as np
>>>
>>> # create measure, topics
>>> measure = 'nlr'
>>> topics = [np.array([1, 2])]
>>>
>>> # create accumulator
>>> dictionary = Dictionary()
>>> dictionary.id2token = {1: 'fake', 2: 'tokens'}
>>> accumulator = text_analysis.WordVectorsAccumulator({1, 2}, dictionary)
>>> _ = accumulator.accumulate([['fake', 'tokens'], ['tokens', 'fake']], 5)
>>> cont_vect_comp = indirect_confirmation_measure.ContextVectorComputer(measure, topics, accumulator, 1)
>>> cont_vect_comp.mapping
{1: 0, 2: 1}
>>> cont_vect_comp.vocab_size
2
compute_context_vector(segment_word_ids, topic_word_ids)

Check if (segment_word_ids, topic_word_ids) context vector has been cached.

Parameters

  • segment_word_ids (list) – Ids of words in segment.

  • topic_word_ids (list) – Ids of words in topic.

Returns

If context vector has been cached, then return corresponding context vector, else compute, cache, and return.

Return type

csr_matrix csr

gensim.topic_coherence.indirect_confirmation_measure.cosine_similarity(segmented_topics, accumulator, topics, measure='nlr', gamma=1, with_std=False, with_support=False)

Calculate the indirect cosine measure.

Parameters

  • segmented_topics (list of lists of (int, numpy.ndarray)) – Output from the segmentation module of the segmented topics.

  • accumulator (InvertedIndexAccumulator) – Output from the probability_estimation module. Is an topics: Topics obtained from the trained topic model.

  • measure (str, optional) – Direct confirmation measure to be used. Supported values are “nlr” (normalized log ratio).

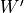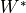  • gamma (float, optional) – Gamma value for computing W' and W^{*} vectors.

  • with_std (bool) – True to also include standard deviation across topic segment sets in addition to the mean coherence for each topic; default is False.

  • with_support (bool) – True to also include support across topic segments. The support is defined as the number of pairwise similarity comparisons were used to compute the overall topic coherence.

Returns

List of indirect cosine similarity measure for each topic.

Return type

list

Examples

>>> from gensim.corpora.dictionary import Dictionary
>>> from gensim.topic_coherence import indirect_confirmation_measure, text_analysis
>>> import numpy as np
>>>
>>> # create accumulator
>>> dictionary = Dictionary()
>>> dictionary.id2token = {1: 'fake', 2: 'tokens'}
>>> accumulator = text_analysis.InvertedIndexAccumulator({1, 2}, dictionary)
>>> accumulator._inverted_index = {0: {2, 3, 4}, 1: {3, 5}}
>>> accumulator._num_docs = 5
>>>
>>> # create topics
>>> topics = [np.array([1, 2])]
>>>
>>> # create segmentation
>>> segmentation = [[(1, np.array([1, 2])), (2, np.array([1, 2]))]]
>>> obtained = indirect_confirmation_measure.cosine_similarity(segmentation, accumulator, topics, 'nlr', 1)
>>> print(obtained[0])
0.623018926945
gensim.topic_coherence.indirect_confirmation_measure.word2vec_similarity(segmented_topics, accumulator, with_std=False, with_support=False)

For each topic segmentation, compute average cosine similarity using a WordVectorsAccumulator.

Parameters

  • segmented_topics (list of lists of (int, numpy.ndarray)) – Output from the s_one_set().

  • accumulator (WordVectorsAccumulator or) – InvertedIndexAccumulator Word occurrence accumulator.

  • with_std (bool, optional) – True to also include standard deviation across topic segment sets in addition to the mean coherence for each topic.

  • with_support (bool, optional) – True to also include support across topic segments. The support is defined as the number of pairwise similarity comparisons were used to compute the overall topic coherence.

Returns

Сosine word2vec similarities per topic (with std/support if with_std, with_support).

Return type

list of (float[, float[, int]])

Examples

>>> import numpy as np
>>> from gensim.corpora.dictionary import Dictionary
>>> from gensim.topic_coherence import indirect_confirmation_measure
>>> from gensim.topic_coherence import text_analysis
>>>
>>> # create segmentation
>>> segmentation = [[(1, np.array([1, 2])), (2, np.array([1, 2]))]]
>>>
>>> # create accumulator
>>> dictionary = Dictionary()
>>> dictionary.id2token = {1: 'fake', 2: 'tokens'}
>>> accumulator = text_analysis.WordVectorsAccumulator({1, 2}, dictionary)
>>> _ = accumulator.accumulate([['fake', 'tokens'], ['tokens', 'fake']], 5)
>>>
>>> # should be (0.726752426218 0.00695475919227)
>>> mean, std = indirect_confirmation_measure.word2vec_similarity(segmentation, accumulator, with_std=True)[0]