models.ldamodel – Latent Dirichlet Allocation¶
Optimized Latent Dirichlet Allocation (LDA) in Python.
For a faster implementation of LDA (parallelized for multicore machines), see also gensim.models.ldamulticore.
This module allows both LDA model estimation from a training corpus and inference of topic distribution on new, unseen documents. The model can also be updated with new documents for online training.
The core estimation code is based on the onlineldavb.py script, by Matthew D. Hoffman, David M. Blei, Francis Bach: ‘Online Learning for Latent Dirichlet Allocation’, NIPS 2010.
The algorithm:
Is streamed: training documents may come in sequentially, no random access required.
Runs in constant memory w.r.t. the number of documents: size of the training corpus does not affect memory footprint, can process corpora larger than RAM.
Is distributed: makes use of a cluster of machines, if available, to speed up model estimation.
Usage examples¶
Train an LDA model using a Gensim corpus
>>> from gensim.test.utils import common_texts
>>> from gensim.corpora.dictionary import Dictionary
>>>
>>> # Create a corpus from a list of texts
>>> common_dictionary = Dictionary(common_texts)
>>> common_corpus = [common_dictionary.doc2bow(text) for text in common_texts]
>>>
>>> # Train the model on the corpus.
>>> lda = LdaModel(common_corpus, num_topics=10)
Save a model to disk, or reload a pre-trained model
>>> from gensim.test.utils import datapath
>>>
>>> # Save model to disk.
>>> temp_file = datapath("model")
>>> lda.save(temp_file)
>>>
>>> # Load a potentially pretrained model from disk.
>>> lda = LdaModel.load(temp_file)
Query, the model using new, unseen documents
>>> # Create a new corpus, made of previously unseen documents.
>>> other_texts = [
... ['computer', 'time', 'graph'],
... ['survey', 'response', 'eps'],
... ['human', 'system', 'computer']
... ]
>>> other_corpus = [common_dictionary.doc2bow(text) for text in other_texts]
>>>
>>> unseen_doc = other_corpus[0]
>>> vector = lda[unseen_doc] # get topic probability distribution for a document
Update the model by incrementally training on the new corpus
>>> lda.update(other_corpus)
>>> vector = lda[unseen_doc]
A lot of parameters can be tuned to optimize training for your specific case
>>> lda = LdaModel(common_corpus, num_topics=50, alpha='auto', eval_every=5) # learn asymmetric alpha from data
- class gensim.models.ldamodel.LdaModel(corpus=None, num_topics=100, id2word=None, distributed=False, chunksize=2000, passes=1, update_every=1, alpha='symmetric', eta=None, decay=0.5, offset=1.0, eval_every=10, iterations=50, gamma_threshold=0.001, minimum_probability=0.01, random_state=None, ns_conf=None, minimum_phi_value=0.01, per_word_topics=False, callbacks=None, dtype=<class 'numpy.float32'>)¶
Bases:
TransformationABC,BaseTopicModelTrain and use Online Latent Dirichlet Allocation model as presented in ‘Online Learning for LDA’ by Hoffman et al.
Examples
Initialize a model using a Gensim corpus
>>> from gensim.test.utils import common_corpus >>> >>> lda = LdaModel(common_corpus, num_topics=10)
You can then infer topic distributions on new, unseen documents.
>>> doc_bow = [(1, 0.3), (2, 0.1), (0, 0.09)] >>> doc_lda = lda[doc_bow]
The model can be updated (trained) with new documents.
>>> # In practice (corpus =/= initial training corpus), but we use the same here for simplicity. >>> other_corpus = common_corpus >>> >>> lda.update(other_corpus)
Model persistency is achieved through
load()andsave()methods.- Parameters
corpus (iterable of list of (int, float), optional) – Stream of document vectors or sparse matrix of shape (num_documents, num_terms). If you have a CSC in-memory matrix, you can convert it to a streamed corpus with the help of gensim.matutils.Sparse2Corpus. If not given, the model is left untrained (presumably because you want to call
update()manually).num_topics (int, optional) – The number of requested latent topics to be extracted from the training corpus.
id2word ({dict of (int, str),
gensim.corpora.dictionary.Dictionary}) – Mapping from word IDs to words. It is used to determine the vocabulary size, as well as for debugging and topic printing.distributed (bool, optional) – Whether distributed computing should be used to accelerate training.
chunksize (int, optional) – Number of documents to be used in each training chunk.
passes (int, optional) – Number of passes through the corpus during training.
update_every (int, optional) – Number of documents to be iterated through for each update. Set to 0 for batch learning, > 1 for online iterative learning.
alpha ({float, numpy.ndarray of float, list of float, str}, optional) –
- A-priori belief on document-topic distribution, this can be:
scalar for a symmetric prior over document-topic distribution,
1D array of length equal to num_topics to denote an asymmetric user defined prior for each topic.
- Alternatively default prior selecting strategies can be employed by supplying a string:
’symmetric’: (default) Uses a fixed symmetric prior of 1.0 / num_topics,
’asymmetric’: Uses a fixed normalized asymmetric prior of 1.0 / (topic_index + sqrt(num_topics)),
’auto’: Learns an asymmetric prior from the corpus (not available if distributed==True).
eta ({float, numpy.ndarray of float, list of float, str}, optional) –
- A-priori belief on topic-word distribution, this can be:
scalar for a symmetric prior over topic-word distribution,
1D array of length equal to num_words to denote an asymmetric user defined prior for each word,
matrix of shape (num_topics, num_words) to assign a probability for each word-topic combination.
- Alternatively default prior selecting strategies can be employed by supplying a string:
’symmetric’: (default) Uses a fixed symmetric prior of 1.0 / num_topics,
’auto’: Learns an asymmetric prior from the corpus.
decay (float, optional) – A number between (0.5, 1] to weight what percentage of the previous lambda value is forgotten when each new document is examined. Corresponds to
 from ‘Online Learning for LDA’ by Hoffman et al.
from ‘Online Learning for LDA’ by Hoffman et al.offset (float, optional) – Hyper-parameter that controls how much we will slow down the first steps the first few iterations. Corresponds to
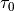 from ‘Online Learning for LDA’ by Hoffman et al.
from ‘Online Learning for LDA’ by Hoffman et al.eval_every (int, optional) – Log perplexity is estimated every that many updates. Setting this to one slows down training by ~2x.
iterations (int, optional) – Maximum number of iterations through the corpus when inferring the topic distribution of a corpus.
gamma_threshold (float, optional) – Minimum change in the value of the gamma parameters to continue iterating.
minimum_probability (float, optional) – Topics with a probability lower than this threshold will be filtered out.
random_state ({np.random.RandomState, int}, optional) – Either a randomState object or a seed to generate one. Useful for reproducibility.
ns_conf (dict of (str, object), optional) – Key word parameters propagated to
gensim.utils.getNS()to get a Pyro4 nameserver. Only used if distributed is set to True.minimum_phi_value (float, optional) – if per_word_topics is True, this represents a lower bound on the term probabilities.
per_word_topics (bool) – If True, the model also computes a list of topics, sorted in descending order of most likely topics for each word, along with their phi values multiplied by the feature length (i.e. word count).
callbacks (list of
Callback) – Metric callbacks to log and visualize evaluation metrics of the model during training.dtype ({numpy.float16, numpy.float32, numpy.float64}, optional) – Data-type to use during calculations inside model. All inputs are also converted.
- __getitem__(bow, eps=None)¶
Get the topic distribution for the given document.
Wraps
get_document_topics()to support an operator style call. Uses the model’s current state (set using constructor arguments) to fill in the additional arguments of the wrapper method.- Parameters
bow (list of (int, float)) – The document in BOW format.
eps (float, optional) – Topics with an assigned probability lower than this threshold will be discarded.
- Returns
Topic distribution for the given document. Each topic is represented as a pair of its ID and the probability assigned to it.
- Return type
list of (int, float)
- add_lifecycle_event(event_name, log_level=20, **event)¶
Append an event into the lifecycle_events attribute of this object, and also optionally log the event at log_level.
Events are important moments during the object’s life, such as “model created”, “model saved”, “model loaded”, etc.
The lifecycle_events attribute is persisted across object’s
save()andload()operations. It has no impact on the use of the model, but is useful during debugging and support.Set self.lifecycle_events = None to disable this behaviour. Calls to add_lifecycle_event() will not record events into self.lifecycle_events then.
- Parameters
event_name (str) – Name of the event. Can be any label, e.g. “created”, “stored” etc.
event (dict) –
Key-value mapping to append to self.lifecycle_events. Should be JSON-serializable, so keep it simple. Can be empty.
This method will automatically add the following key-values to event, so you don’t have to specify them:
datetime: the current date & time
gensim: the current Gensim version
python: the current Python version
platform: the current platform
event: the name of this event
log_level (int) – Also log the complete event dict, at the specified log level. Set to False to not log at all.
- bound(corpus, gamma=None, subsample_ratio=1.0)¶
Estimate the variational bound of documents from the corpus as E_q[log p(corpus)] - E_q[log q(corpus)].
- Parameters
corpus (iterable of list of (int, float), optional) – Stream of document vectors or sparse matrix of shape (num_documents, num_terms) used to estimate the variational bounds.
gamma (numpy.ndarray, optional) – Topic weight variational parameters for each document. If not supplied, it will be inferred from the model.
subsample_ratio (float, optional) – Percentage of the whole corpus represented by the passed corpus argument (in case this was a sample). Set to 1.0 if the whole corpus was passed.This is used as a multiplicative factor to scale the likelihood appropriately.
- Returns
The variational bound score calculated for each document.
- Return type
numpy.ndarray
- clear()¶
Clear the model’s state to free some memory. Used in the distributed implementation.
- diff(other, distance='kullback_leibler', num_words=100, n_ann_terms=10, diagonal=False, annotation=True, normed=True)¶
Calculate the difference in topic distributions between two models: self and other.
- Parameters
other (
LdaModel) – The model which will be compared against the current object.distance ({'kullback_leibler', 'hellinger', 'jaccard', 'jensen_shannon'}) – The distance metric to calculate the difference with.
num_words (int, optional) – The number of most relevant words used if distance == ‘jaccard’. Also used for annotating topics.
n_ann_terms (int, optional) – Max number of words in intersection/symmetric difference between topics. Used for annotation.
diagonal (bool, optional) – Whether we need the difference between identical topics (the diagonal of the difference matrix).
annotation (bool, optional) – Whether the intersection or difference of words between two topics should be returned.
normed (bool, optional) – Whether the matrix should be normalized or not.
- Returns
numpy.ndarray – A difference matrix. Each element corresponds to the difference between the two topics, shape (self.num_topics, other.num_topics)
numpy.ndarray, optional – Annotation matrix where for each pair we include the word from the intersection of the two topics, and the word from the symmetric difference of the two topics. Only included if annotation == True. Shape (self.num_topics, other_model.num_topics, 2).
Examples
Get the differences between each pair of topics inferred by two models
>>> from gensim.models.ldamulticore import LdaMulticore >>> from gensim.test.utils import datapath >>> >>> m1 = LdaMulticore.load(datapath("lda_3_0_1_model")) >>> m2 = LdaMulticore.load(datapath("ldamodel_python_3_5")) >>> mdiff, annotation = m1.diff(m2) >>> topic_diff = mdiff # get matrix with difference for each topic pair from `m1` and `m2`
- do_estep(chunk, state=None)¶
Perform inference on a chunk of documents, and accumulate the collected sufficient statistics.
- Parameters
chunk (list of list of (int, float)) – The corpus chunk on which the inference step will be performed.
state (
LdaState, optional) – The state to be updated with the newly accumulated sufficient statistics. If none, the models self.state is updated.
- Returns
Gamma parameters controlling the topic weights, shape (len(chunk), self.num_topics).
- Return type
numpy.ndarray
- do_mstep(rho, other, extra_pass=False)¶
Maximization step: use linear interpolation between the existing topics and collected sufficient statistics in other to update the topics.
- Parameters
rho (float) – Learning rate.
other (
LdaModel) – The model whose sufficient statistics will be used to update the topics.extra_pass (bool, optional) – Whether this step required an additional pass over the corpus.
- get_document_topics(bow, minimum_probability=None, minimum_phi_value=None, per_word_topics=False)¶
Get the topic distribution for the given document.
- Parameters
bow (corpus : list of (int, float)) – The document in BOW format.
minimum_probability (float) – Topics with an assigned probability lower than this threshold will be discarded.
minimum_phi_value (float) –
- If per_word_topics is True, this represents a lower bound on the term probabilities that are included.
If set to None, a value of 1e-8 is used to prevent 0s.
per_word_topics (bool) – If True, this function will also return two extra lists as explained in the “Returns” section.
- Returns
list of (int, float) – Topic distribution for the whole document. Each element in the list is a pair of a topic’s id, and the probability that was assigned to it.
list of (int, list of (int, float), optional – Most probable topics per word. Each element in the list is a pair of a word’s id, and a list of topics sorted by their relevance to this word. Only returned if per_word_topics was set to True.
list of (int, list of float), optional – Phi relevance values, multiplied by the feature length, for each word-topic combination. Each element in the list is a pair of a word’s id and a list of the phi values between this word and each topic. Only returned if per_word_topics was set to True.
- get_term_topics(word_id, minimum_probability=None)¶
Get the most relevant topics to the given word.
- Parameters
word_id (int) – The word for which the topic distribution will be computed.
minimum_probability (float, optional) – Topics with an assigned probability below this threshold will be discarded.
- Returns
The relevant topics represented as pairs of their ID and their assigned probability, sorted by relevance to the given word.
- Return type
list of (int, float)
- get_topic_terms(topicid, topn=10)¶
Get the representation for a single topic. Words the integer IDs, in constrast to
show_topic()that represents words by the actual strings.- Parameters
topicid (int) – The ID of the topic to be returned
topn (int, optional) – Number of the most significant words that are associated with the topic.
- Returns
Word ID - probability pairs for the most relevant words generated by the topic.
- Return type
list of (int, float)
- get_topics()¶
Get the term-topic matrix learned during inference.
- Returns
The probability for each word in each topic, shape (num_topics, vocabulary_size).
- Return type
numpy.ndarray
- inference(chunk, collect_sstats=False)¶
Given a chunk of sparse document vectors, estimate gamma (parameters controlling the topic weights) for each document in the chunk.
This function does not modify the model. The whole input chunk of document is assumed to fit in RAM; chunking of a large corpus must be done earlier in the pipeline. Avoids computing the phi variational parameter directly using the optimization presented in Lee, Seung: Algorithms for non-negative matrix factorization”.
- Parameters
chunk (list of list of (int, float)) – The corpus chunk on which the inference step will be performed.
collect_sstats (bool, optional) – If set to True, also collect (and return) sufficient statistics needed to update the model’s topic-word distributions.
- Returns
The first element is always returned and it corresponds to the states gamma matrix. The second element is only returned if collect_sstats == True and corresponds to the sufficient statistics for the M step.
- Return type
(numpy.ndarray, {numpy.ndarray, None})
- init_dir_prior(prior, name)¶
Initialize priors for the Dirichlet distribution.
- Parameters
prior ({float, numpy.ndarray of float, list of float, str}) –
- A-priori belief on document-topic distribution. If name == ‘alpha’, then the prior can be:
scalar for a symmetric prior over document-topic distribution,
1D array of length equal to num_topics to denote an asymmetric user defined prior for each topic.
- Alternatively default prior selecting strategies can be employed by supplying a string:
’symmetric’: (default) Uses a fixed symmetric prior of 1.0 / num_topics,
’asymmetric’: Uses a fixed normalized asymmetric prior of 1.0 / (topic_index + sqrt(num_topics)),
’auto’: Learns an asymmetric prior from the corpus (not available if distributed==True).
- A-priori belief on topic-word distribution. If name == ‘eta’ then the prior can be:
scalar for a symmetric prior over topic-word distribution,
1D array of length equal to num_words to denote an asymmetric user defined prior for each word,
matrix of shape (num_topics, num_words) to assign a probability for each word-topic combination.
- Alternatively default prior selecting strategies can be employed by supplying a string:
’symmetric’: (default) Uses a fixed symmetric prior of 1.0 / num_topics,
’auto’: Learns an asymmetric prior from the corpus.
name ({'alpha', 'eta'}) – Whether the prior is parameterized by the alpha vector (1 parameter per topic) or by the eta (1 parameter per unique term in the vocabulary).
- Returns
init_prior (numpy.ndarray) – Initialized Dirichlet prior: If ‘alpha’ was provided as name the shape is (self.num_topics, ). If ‘eta’ was provided as name the shape is (len(self.id2word), ).
is_auto (bool) – Flag that shows if hyperparameter optimization should be used or not.
- classmethod load(fname, *args, **kwargs)¶
Load a previously saved
gensim.models.ldamodel.LdaModelfrom file.See also
save()Save model.
- Parameters
Examples
Large arrays can be memmap’ed back as read-only (shared memory) by setting mmap=’r’:
>>> from gensim.test.utils import datapath >>> >>> fname = datapath("lda_3_0_1_model") >>> lda = LdaModel.load(fname, mmap='r')
- log_perplexity(chunk, total_docs=None)¶
Calculate and return per-word likelihood bound, using a chunk of documents as evaluation corpus.
Also output the calculated statistics, including the perplexity=2^(-bound), to log at INFO level.
- Parameters
chunk (list of list of (int, float)) – The corpus chunk on which the inference step will be performed.
total_docs (int, optional) – Number of docs used for evaluation of the perplexity.
- Returns
The variational bound score calculated for each word.
- Return type
numpy.ndarray
- print_topic(topicno, topn=10)¶
Get a single topic as a formatted string.
- Parameters
topicno (int) – Topic id.
topn (int) – Number of words from topic that will be used.
- Returns
String representation of topic, like ‘-0.340 * “category” + 0.298 * “$M$” + 0.183 * “algebra” + … ‘.
- Return type
str
- print_topics(num_topics=20, num_words=10)¶
Get the most significant topics (alias for show_topics() method).
- Parameters
num_topics (int, optional) – The number of topics to be selected, if -1 - all topics will be in result (ordered by significance).
num_words (int, optional) – The number of words to be included per topics (ordered by significance).
- Returns
Sequence with (topic_id, [(word, value), … ]).
- Return type
list of (int, list of (str, float))
- save(fname, ignore=('state', 'dispatcher'), separately=None, *args, **kwargs)¶
Save the model to a file.
Large internal arrays may be stored into separate files, with fname as prefix.
Notes
If you intend to use models across Python 2/3 versions there are a few things to keep in mind:
The pickled Python dictionaries will not work across Python versions
The save method does not automatically save all numpy arrays separately, only those ones that exceed sep_limit set in
save(). The main concern here is the alpha array if for instance using alpha=’auto’.
Please refer to the wiki recipes section for an example on how to work around these issues.
See also
load()Load model.
- Parameters
fname (str) – Path to the system file where the model will be persisted.
ignore (tuple of str, optional) – The named attributes in the tuple will be left out of the pickled model. The reason why the internal state is ignored by default is that it uses its own serialisation rather than the one provided by this method.
separately ({list of str, None}, optional) – If None - automatically detect large numpy/scipy.sparse arrays in the object being stored, and store them into separate files. This avoids pickle memory errors and allows mmap’ing large arrays back on load efficiently. If list of str - this attributes will be stored in separate files, the automatic check is not performed in this case.
*args – Positional arguments propagated to
save().**kwargs – Key word arguments propagated to
save().
- show_topic(topicid, topn=10)¶
Get the representation for a single topic. Words here are the actual strings, in constrast to
get_topic_terms()that represents words by their vocabulary ID.- Parameters
topicid (int) – The ID of the topic to be returned
topn (int, optional) – Number of the most significant words that are associated with the topic.
- Returns
Word - probability pairs for the most relevant words generated by the topic.
- Return type
list of (str, float)
- show_topics(num_topics=10, num_words=10, log=False, formatted=True)¶
Get a representation for selected topics.
- Parameters
num_topics (int, optional) – Number of topics to be returned. Unlike LSA, there is no natural ordering between the topics in LDA. The returned topics subset of all topics is therefore arbitrary and may change between two LDA training runs.
num_words (int, optional) – Number of words to be presented for each topic. These will be the most relevant words (assigned the highest probability for each topic).
log (bool, optional) – Whether the output is also logged, besides being returned.
formatted (bool, optional) – Whether the topic representations should be formatted as strings. If False, they are returned as 2 tuples of (word, probability).
- Returns
a list of topics, each represented either as a string (when formatted == True) or word-probability pairs.
- Return type
list of {str, tuple of (str, float)}
- sync_state(current_Elogbeta=None)¶
Propagate the states topic probabilities to the inner object’s attribute.
- Parameters
current_Elogbeta (numpy.ndarray) – Posterior probabilities for each topic, optional. If omitted, it will get Elogbeta from state.
- top_topics(corpus=None, texts=None, dictionary=None, window_size=None, coherence='u_mass', topn=20, processes=-1)¶
Get the topics with the highest coherence score the coherence for each topic.
- Parameters
corpus (iterable of list of (int, float), optional) – Corpus in BoW format.
texts (list of list of str, optional) – Tokenized texts, needed for coherence models that use sliding window based (i.e. coherence=`c_something`) probability estimator .
dictionary (
Dictionary, optional) – Gensim dictionary mapping of id word to create corpus. If model.id2word is present, this is not needed. If both are provided, passed dictionary will be used.window_size (int, optional) – Is the size of the window to be used for coherence measures using boolean sliding window as their probability estimator. For ‘u_mass’ this doesn’t matter. If None - the default window sizes are used which are: ‘c_v’ - 110, ‘c_uci’ - 10, ‘c_npmi’ - 10.
coherence ({'u_mass', 'c_v', 'c_uci', 'c_npmi'}, optional) – Coherence measure to be used. Fastest method - ‘u_mass’, ‘c_uci’ also known as c_pmi. For ‘u_mass’ corpus should be provided, if texts is provided, it will be converted to corpus using the dictionary. For ‘c_v’, ‘c_uci’ and ‘c_npmi’ texts should be provided (corpus isn’t needed)
topn (int, optional) – Integer corresponding to the number of top words to be extracted from each topic.
processes (int, optional) – Number of processes to use for probability estimation phase, any value less than 1 will be interpreted as num_cpus - 1.
- Returns
Each element in the list is a pair of a topic representation and its coherence score. Topic representations are distributions of words, represented as a list of pairs of word IDs and their probabilities.
- Return type
list of (list of (int, str), float)
- update(corpus, chunksize=None, decay=None, offset=None, passes=None, update_every=None, eval_every=None, iterations=None, gamma_threshold=None, chunks_as_numpy=False)¶
Train the model with new documents, by EM-iterating over the corpus until the topics converge, or until the maximum number of allowed iterations is reached. corpus must be an iterable.
In distributed mode, the E step is distributed over a cluster of machines.
Notes
This update also supports updating an already trained model (self) with new documents from corpus; the two models are then merged in proportion to the number of old vs. new documents. This feature is still experimental for non-stationary input streams.
For stationary input (no topic drift in new documents), on the other hand, this equals the online update of ‘Online Learning for LDA’ by Hoffman et al. and is guaranteed to converge for any decay in (0.5, 1]. Additionally, for smaller corpus sizes, an increasing offset may be beneficial (see Table 1 in the same paper).
- Parameters
corpus (iterable of list of (int, float), optional) – Stream of document vectors or sparse matrix of shape (num_documents, num_terms) used to update the model.
chunksize (int, optional) – Number of documents to be used in each training chunk.
decay (float, optional) – A number between (0.5, 1] to weight what percentage of the previous lambda value is forgotten when each new document is examined. Corresponds to
 from
‘Online Learning for LDA’ by Hoffman et al.
from
‘Online Learning for LDA’ by Hoffman et al.offset (float, optional) – Hyper-parameter that controls how much we will slow down the first steps the first few iterations. Corresponds to
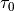 from ‘Online Learning for LDA’ by Hoffman et al.
from ‘Online Learning for LDA’ by Hoffman et al.passes (int, optional) – Number of passes through the corpus during training.
update_every (int, optional) – Number of documents to be iterated through for each update. Set to 0 for batch learning, > 1 for online iterative learning.
eval_every (int, optional) – Log perplexity is estimated every that many updates. Setting this to one slows down training by ~2x.
iterations (int, optional) – Maximum number of iterations through the corpus when inferring the topic distribution of a corpus.
gamma_threshold (float, optional) – Minimum change in the value of the gamma parameters to continue iterating.
chunks_as_numpy (bool, optional) – Whether each chunk passed to the inference step should be a numpy.ndarray or not. Numpy can in some settings turn the term IDs into floats, these will be converted back into integers in inference, which incurs a performance hit. For distributed computing it may be desirable to keep the chunks as numpy.ndarray.
- update_alpha(gammat, rho)¶
Update parameters for the Dirichlet prior on the per-document topic weights.
- Parameters
gammat (numpy.ndarray) – Previous topic weight parameters.
rho (float) – Learning rate.
- Returns
Sequence of alpha parameters.
- Return type
numpy.ndarray
- update_eta(lambdat, rho)¶
Update parameters for the Dirichlet prior on the per-topic word weights.
- Parameters
lambdat (numpy.ndarray) – Previous lambda parameters.
rho (float) – Learning rate.
- Returns
The updated eta parameters.
- Return type
numpy.ndarray
- class gensim.models.ldamodel.LdaState(eta, shape, dtype=<class 'numpy.float32'>)¶
Bases:
SaveLoadEncapsulate information for distributed computation of
LdaModelobjects.Objects of this class are sent over the network, so try to keep them lean to reduce traffic.
- Parameters
eta (numpy.ndarray) – The prior probabilities assigned to each term.
shape (tuple of (int, int)) – Shape of the sufficient statistics: (number of topics to be found, number of terms in the vocabulary).
dtype (type) – Overrides the numpy array default types.
- add_lifecycle_event(event_name, log_level=20, **event)¶
Append an event into the lifecycle_events attribute of this object, and also optionally log the event at log_level.
Events are important moments during the object’s life, such as “model created”, “model saved”, “model loaded”, etc.
The lifecycle_events attribute is persisted across object’s
save()andload()operations. It has no impact on the use of the model, but is useful during debugging and support.Set self.lifecycle_events = None to disable this behaviour. Calls to add_lifecycle_event() will not record events into self.lifecycle_events then.
- Parameters
event_name (str) – Name of the event. Can be any label, e.g. “created”, “stored” etc.
event (dict) –
Key-value mapping to append to self.lifecycle_events. Should be JSON-serializable, so keep it simple. Can be empty.
This method will automatically add the following key-values to event, so you don’t have to specify them:
datetime: the current date & time
gensim: the current Gensim version
python: the current Python version
platform: the current platform
event: the name of this event
log_level (int) – Also log the complete event dict, at the specified log level. Set to False to not log at all.
- blend(rhot, other, targetsize=None)¶
Merge the current state with another one using a weighted average for the sufficient statistics.
The number of documents is stretched in both state objects, so that they are of comparable magnitude. This procedure corresponds to the stochastic gradient update from ‘Online Learning for LDA’ by Hoffman et al., see equations (5) and (9).
- Parameters
rhot (float) – Weight of the other state in the computed average. A value of 0.0 means that other is completely ignored. A value of 1.0 means self is completely ignored.
other (
LdaState) – The state object with which the current one will be merged.targetsize (int, optional) – The number of documents to stretch both states to.
- blend2(rhot, other, targetsize=None)¶
Merge the current state with another one using a weighted sum for the sufficient statistics.
In contrast to
blend(), the sufficient statistics are not scaled prior to aggregation.- Parameters
rhot (float) – Unused.
other (
LdaState) – The state object with which the current one will be merged.targetsize (int, optional) – The number of documents to stretch both states to.
- get_Elogbeta()¶
Get the log (posterior) probabilities for each topic.
- Returns
Posterior probabilities for each topic.
- Return type
numpy.ndarray
- get_lambda()¶
Get the parameters of the posterior over the topics, also referred to as “the topics”.
- Returns
Parameters of the posterior probability over topics.
- Return type
numpy.ndarray
- classmethod load(fname, *args, **kwargs)¶
Load a previously stored state from disk.
Overrides
loadby enforcing the dtype parameter to ensure backwards compatibility.- Parameters
fname (str) – Path to file that contains the needed object.
args (object) – Positional parameters to be propagated to class:~gensim.utils.SaveLoad.load
kwargs (object) – Key-word parameters to be propagated to class:~gensim.utils.SaveLoad.load
- Returns
The state loaded from the given file.
- Return type
- merge(other)¶
Merge the result of an E step from one node with that of another node (summing up sufficient statistics).
The merging is trivial and after merging all cluster nodes, we have the exact same result as if the computation was run on a single node (no approximation).
- Parameters
other (
LdaState) – The state object with which the current one will be merged.
- reset()¶
Prepare the state for a new EM iteration (reset sufficient stats).
- save(fname_or_handle, separately=None, sep_limit=10485760, ignore=frozenset({}), pickle_protocol=4)¶
Save the object to a file.
- Parameters
fname_or_handle (str or file-like) – Path to output file or already opened file-like object. If the object is a file handle, no special array handling will be performed, all attributes will be saved to the same file.
separately (list of str or None, optional) –
If None, automatically detect large numpy/scipy.sparse arrays in the object being stored, and store them into separate files. This prevent memory errors for large objects, and also allows memory-mapping the large arrays for efficient loading and sharing the large arrays in RAM between multiple processes.
If list of str: store these attributes into separate files. The automated size check is not performed in this case.
sep_limit (int, optional) – Don’t store arrays smaller than this separately. In bytes.
ignore (frozenset of str, optional) – Attributes that shouldn’t be stored at all.
pickle_protocol (int, optional) – Protocol number for pickle.
See also
load()Load object from file.
- gensim.models.ldamodel.update_dir_prior(prior, N, logphat, rho)¶
Update a given prior using Newton’s method, described in J. Huang: “Maximum Likelihood Estimation of Dirichlet Distribution Parameters”.
- Parameters
prior (list of float) – The prior for each possible outcome at the previous iteration (to be updated).
N (int) – Number of observations.
logphat (list of float) – Log probabilities for the current estimation, also called “observed sufficient statistics”.
rho (float) – Learning rate.
- Returns
The updated prior.
- Return type
list of float
